Kernel-based Translations of Convolutional Networks
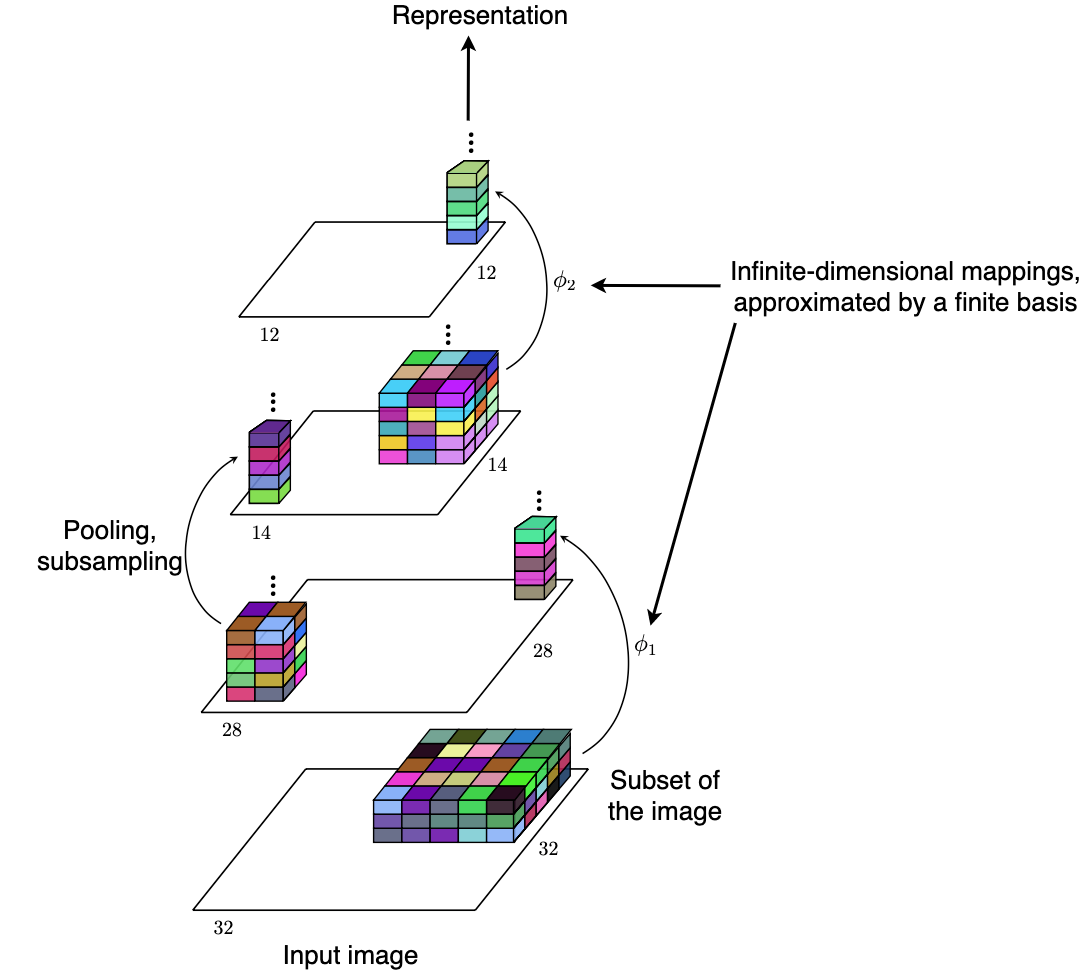
In [2], we develop statistical models that can be seen as kernel-based counterparts of convolutional neural networks. The approach hinges upon the connection between a layer of a neural network and the Nyström quadrature approximation of an associated integral operator. Owing to this connection, we can translate classical convolutional neural networks, such as LeNet, All-CNN, or AlexNet, into corresponding convolutional kernel network counterparts. The resulting networks then implement functional mappings living in clearly-defined reproducing kernel Hilbert spaces. We provide a gradient-based stochastic training algorithm that allows one to estimate the parameters of the proposed convolutional kernel networks. The methods and the algorithms are illustrated on several benchmark datasets in image classification.
Results
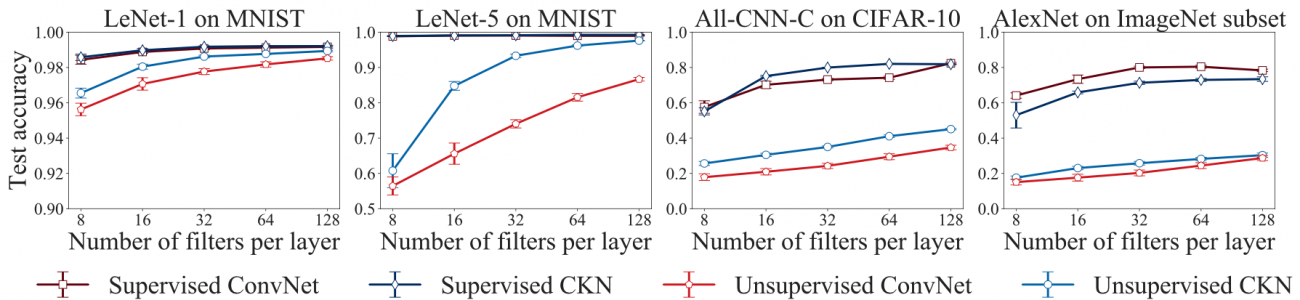
We compare in the test accuracies of Convolutional Neural Networks (ConvNets) to the test accuracies of the corresponding Convolutional Kernel Networks (CKNs) on classical benchmark datasets in image classification (MNIST, CIFAR10, ImageNet), with landmark architectures (LeNet-1, LeNet-5, All-CNN, AlexNet). We compare the accuracies for varying numbers of filters. For CKNs, the number of filters controls the quality of the Nyström quadrature approximation of the kernel. We may expect an increase of performance for a larger number of filters. The results present the performances in (a) a supervised setting where the parameters of the network are learned from labeled data, (b) an unsupervised setting where the network parameters are computed from unlabeled data.
References
[1] Jones, C., Roulet, V. and Harchaoui, Z., 2020. Discriminative Clustering with Representation Learning with any Ratio of Labeled to Unlabeled Data. In revision.
[2] Jones, C., Roulet, V. and Harchaoui, Z., 2019. Kernel-based Translations of Convolutional Networks. arXiv preprint arXiv:1903.08131. (Bibtex)
Acknowledgments
These works were supported by NSF TRIPODS Award CCF-1740551, NSF DMS-1810975, NSF IIS-1833154, CCF-2019844 the program “Learning in Machines and Brains” of CIFAR, and faculty research awards.